These multiplication sequences are the main area of my interest with the cube. Each number has a pattern that it repeats within 16 parts. On each of the number’s profiles I’ll go into further detail about my thoughts on how it repeats. There will also be sections about the odds and even numbers as a whole, as well as for each of the shapes and marks and how that effects the sequence.
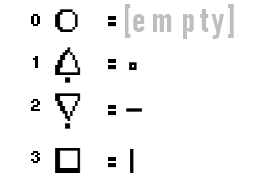
While talking about the sequence patterns, I’ll refer to each of the shapes and marks using their “numeric equivalents” of 0-3.
This equivalent becomes important when you look at the 1st, 4th, 8th and 12th place in each sequence. The starting “shape” will always follow the same pattern that the shape’s mark would follow. I’ll refer to these placements in the sequence as the “Quadrant Sequence”
All empty shapes have empty products.
All dotted shapes go in a 0 – 1 – 2 – 3 pattern
All dashed shapes go in a 0 – 2 – 0 – 2 pattern
All slashed shapes go in a 0 – 3 – 2 – 1 pattern
The sections in red are the “minimum repeatable pattern“, or “MRP” and are what will continue on infinitely.

0 is basically itself for all eternity. It doesn’t even increase to the 1’s place.

1 has the simplest, most straightforward pattern. Both the shapes and marks increase going 0-1-2-3
It doesn’t reach the 10’s place until it completes its MRP, and is the only odd number to do so.
2, 4 and 8 are the other exceptions to this increase.

2 is very balanced, its marks & quadrants go in a 0 – 2 – 0 -2 pattern, like all subsequent “dashed” numbers.
The shapes still increase in a 0 – 1 – 2 – 3 pattern, but each shape counts up in doubles. Very true to 2!
It doesn’t reach the 10s until it completes its MRP much like 1, 4 and 8.
It completes its MRP in 8 ( 2/16= 8), while 4 does in 4, and 8 does in 2.
This relationship relates to how the numbers square and branch off from binary.

3’s marks & quadrants go 0 – 3 – 2 – 1.
3 is the first number to include the 10’s place in its MRP.
The shapes still go 0 – 1 – 2 – 3… but quadrants interactions are interesting, as are all odd-primes.
The starting shape will always be the one absent in the previous quadrant, and the last 2 shapes will be the middle-2 shapes from the previous quadrant.
0 – 0 – 1 – 2 ~ 3 – 3 – 0 – 1 ~ 2 – 2 – 3 – 0 ~ 1 – 1 – 2 – 3

4’s set is entirely empty, but the shapes increase in a 0-1-2-3 pattern. It doesn’t reach the 10s place until it completes its MRP, much like 1, 2 and 8.
4 completes its MRP in 4 (16/4 = 4), while 2 does in 8, and 8 does in 2.
This relationship relates to how the numbers square and branch off from binary.
Also, since it’s “1” in base-4, it’s interesting that it would resemble a more “compact” version of base-16’s “1”.

5’s marks & quadrants increase in a 0 – 1 – 2 – 3 pattern like all dotted shapes.
The shapes no longer increase in a 0 – 1 – 2 – 3 pattern, though they follow the general flow of it. Each quadrant will include all the shapes, but the first 3 shapes will be the last 3 of the previous quadrant, and the previous quadrant’s first-shape will then become the last shape.
0 – 1- 2- 3 ~ 1 – 2 – 3 – 0 ~ 2 – 3 – 0 – 1 ~ 3 – 2 – 1 – 0

6 is the first number with both an odd and even factor. It’s 2 * 3, and is also 3/8 of 16.
In larger multiplications, you can see how 3 influences 6 quite strongly.
On this scale though, like the other dashed numbers, its marks and quadrants follow a 0 – 2 – 0 – 2 pattern.
The shapes have a very stable pattern. It uses 2 quadrants, and basically flips its shapes between the two. The first and last shapes will be either 0 or 2, and the middle shapes will always be 1 and 3.
0 – 1 – 3 – 0 ~ 2 – 3 – 1 – 2

7 is another odd-prime. The marks go in a 0 – 3 – 2 – 1 order, like all slashed shapes.
The shapes have a really unique pattern though. The 3rd shape will always be the first shape in the next quadrant, and the first shape will be the next quadrant’s 2nd and 4th shapes. The 3rd shape will be the next one in the 0 – 3 – 2 – 1 sequence, relative to the first number in the quadrant.
0 – 1 – 3 – 1 ~ 3 – 0 – 2 – 0 ~ 2 – 3 – 1 – 3 ~ 1 – 2 – 0 – 2

In its branching off nature, 8 represents where binary’s “0” and “1” split off in base-16, as the halfway point (16/2=8).
It’s also “2” in base-4, which is fitting of it’s heavy 0-2 pattern. Even in the 10s place, it neatly increases every-other place. It’s the only shape that only has 2 shapes in it’s shape-pattern. It’s MRP is the shortest of all the numbers, save for 0.

9 is the square of 3, and the first prime number with 2 odd factors in the cube. This is the first number where you see an immediate increase in the 10s place from number to number (in the 3rd and 4th-1st quadrants)
It’s marks increase in a 0 – 1 – 2 – 3 pattern like all dots. The shapes have a very tidy repetition, with only 2-alternating shapes per quadrant.
The first and second quadrants are even ( 0 & 2), and the 2nd and 4th are odd (1 & 3).
0 – 2 – 0 – 2 ~ 1 – 3 – 1 – 3 ~ 2 – 0 – 2 – 0 ~ 3 – 1 – 3 – 1

10, or “A” is 5 * 2, and 5/8ths of 16. When you see it in larger multiplications, 5’s influence becomes apparent.
Like all dashed shapes though, its marks will go in a 0 – 2 – 0 – 2 pattern.
Like 5, A also includes a full set of the shapes in each quadrant.
In each quadrant, the first 2 shapes are the evens and the last 2 are the odds. They reverse their order between quadrants.
0 – 2 – 1 – 3 ~ 2 – 0 – 3 – 1

11, or “B” is a prime-odd number. It’s marks, like all slashed shapes, goes in a 0-3-2-1 pattern.
In each quadrant, the 1st and 4th shape are the same. The first of the middle shapes will always be +2 from the first shape, and the one next to it will always be the 2nd shape minus 1, and the beginning shape in the next quadrant will be an additional -1. The bold number replaces “x” in this formula as it repeats…
x + 2 – 1 – 1 – 1
0 – 2 – 1 – 0 ~ 3 – 1 – 0 – 3 ~ 2 – 0 – 3 – 2 ~ 1 – 3 – 2 – 1

12, or “C” is the last of the empty shapes, and is 4 * 3. You can see the 4’s factor in it, from it’s MRP being completed in 4.
It’s also interesting that C is 3/4 of 16, even though 16 isn’t divisible by 12. It relates to how 4 is 1/4, and 8 is 1/2 of 16 though.
It’s the first one that has the 10s increasing 3-times in a row.
Since it’s the “3” in base-4, it makes sense that its MRP goes 0-3-2-1 as well.

13, or “D” is an odd-prime number, and like all the dots has its marks go in a “0-1-2-3” order.
It’s the first one to have the 10s increase 4-times and 5 in a row.
The shapes patterns are interesting because it’s the first one to have the shapes repeat into the following quadrant, while keeping true to the mark-quad pattern. Each quadrant has a full set of shapes, and much like 11, has a very neat formula for its quadrants. The bold one replaces “x” when it repeats.
x + 3 – 1 – 1 = y
0 – 3 – 2 – 1 ~ 1 – 0 – 3 -2 ~ 2 – 1 – 0 – 3 ~ 3 – 2 – 1 – 0

14, or “E” is 7 * 2, and a very neat number. Like all dashed numbers, its marks go ” 0 – 2 – 0 – 2 “. A lot like the number 2, its shapes go in doubled up patterns, but in the reverse of 2 ( 0 – 3 – 2 – 1 ). It’s 7/8ths of 16 as well. It makes a jump straight from having the 10s increase 4-in a row to 7 in a row as well.

15, or “F” is made of 3 * 5, and besides 9, is the only number with 2 odd factors. I find it fascinating that it mirrors 1 in reverse (much like E and 2). The marks and shapes both go in an order of 0-3-2-1, and the 10s increase every place for 15-places.

10 is just like the 10 we all know and use! Just add a 0 onto whatever you’re multiplying, and there you go. It’s just like multiplying by 1.
